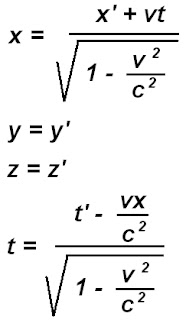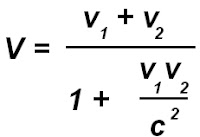Перетворення Галілея та механічний принцип відносності
 | |
| Галілео Галілей (1564 - 1642) |
Розглянемо дві системи відліку (СВ): інерціальна система відліку XYZ, яка є нерухомою, та рухому інерціальну систему відліку X’Y’Z’ , котра рухається поступально зі швидкістю u' вздовж осі ОX. Нехай точки О, О’ в момент часу t0 = 0 співпадають.
Положення довільної точки М в рухомій та нерухомій СВ визначаються відповідно:
К (XYZ): М(x,y,z) К'(X'Y'Z'): M'(x',y',z').
Перетворення координат між СВ К та К’
x = x'+ ut
y = y'
z = z'
називаються перетвореннями Галілея.
Якщо в системі К знаходиться лінійка АВ, довжини l = x2 – x1, то в рухомій системі К’ її довжина відповідно дорівнює:
l' = x2' – x1' = ( x2 – ut) – ( x1 – ut ) = x2 – x1 = l
Сукупність перетворень Галілея слід доповнити ще одним рівнянням, котре не завжди записують, однак воно має велике значення і глибокий зміст:
t = t'
В класичній (ньютонівській) механіці приймається, що хід часу не залежить від відносного руху систем відліку, тобто він є однаковим у всіх інерціальних системах відліку ( системах, котрі рухаються рівномірно і поступально одна відносно іншої).
Нехай точка М(x',y',z') в системі К' рухається зі швидкістю v вздовж осі Ох. За час Δt вона здійснить переміщення S1, а сама система К' переміститься відносно К на вектор переміщення S2. Загальне переміщення S в абсолютній системі координат:
S = S1 + S2
Поділивши останнє співвідношення на час Δt отримаємо класичний закон додавання швидкостей
v= v1 + v2
Вперше його отримав Галілей в 1638 році.
Сутність перетворень Галілея полягає в тому, що якщо ми маємо інерціальну систему відліку К , то довільна система К’, котра рухається відносно К прямолінійно та рівномірно, буде також інерціальною.
А саме для інерціальних систем справедливим є механічний принцип відносності:
У всіх ІСВ всі механічні явища протікають однаково.
Вперше його сформулював Г.Галілей у 1590 році, і він виконується в рамках класичної механіки.
[При переході до механіки великих швидкостей – релятивістської механіки – перетворення Галілея не виконуються. Правильними будуть перетворення Лоренца ( перетворення Галілея є граничним випадком перетворень Лоренца при v<< c).
І релятивістський закон додавання швидкостей набуває вигляду
Відзначу, що довжина відрізка АВ в рухомій СВ змінить свою величину, як і проміжок часу між двома подіями – час в різних ІСВ протікає по-різному. Саме цей висновок надає нам теоретичну можливість переміщуватись у часі.]
В основному тексті жирнішим шрифтом виділено векторні величини.